Introduction
Diffusion models have revolutionized generative modeling in vision, achieving state-of-the-art results in image generation and manipulation. However, applying diffusion directly to language presents a fundamental challenge: text is inherently discrete, while diffusion processes are naturally suited to continuous data. This paper, arXiv:2212.09462, proposes a solution by introducing latent diffusion for natural language generation—a framework that performs diffusion in learned continuous latent spaces rather than on discrete tokens. By bridging the gap between the continuous nature of diffusion and the discrete nature of language, the authors achieve efficient, high-quality text generation with unprecedented control over the generation process.
The Challenge: Diffusion Meets Discrete Language
Standard diffusion models operate on continuous data through an iterative corruption and denoising process:
$$x_t = \sqrt{1-\beta_t} x_{t-1} + \sqrt{\beta_t} \epsilon, \quad \epsilon \sim \mathcal{N}(0, I)$$
where $\beta_t$ is the noise schedule controlling the amount of Gaussian noise added at each step. However, language is fundamentally discrete—each token belongs to a finite vocabulary. Applying diffusion to discrete tokens directly creates several challenges:
1. Non-differentiability: Discrete tokens cannot be smoothly interpolated. Small noise perturbations do not produce meaningful intermediate states—they produce undefined or out-of-vocabulary results.
2. Vocabulary Sparsity: Text operates in a high-dimensional discrete space (vocabulary size × sequence length). Adding noise over this space is inefficient and does not leverage the structure of language.
3. Inefficient Reverse Process: Recovering meaningful text from maximally noised discrete tokens is substantially harder than recovering images from noise, as the information density is far lower in discrete spaces.
Existing approaches attempted to address this by applying diffusion directly to embeddings or using categorical distributions over the vocabulary. The authors identify that these approaches are inefficient and suboptimal—instead, they propose learning a separate latent space where diffusion becomes natural and efficient.
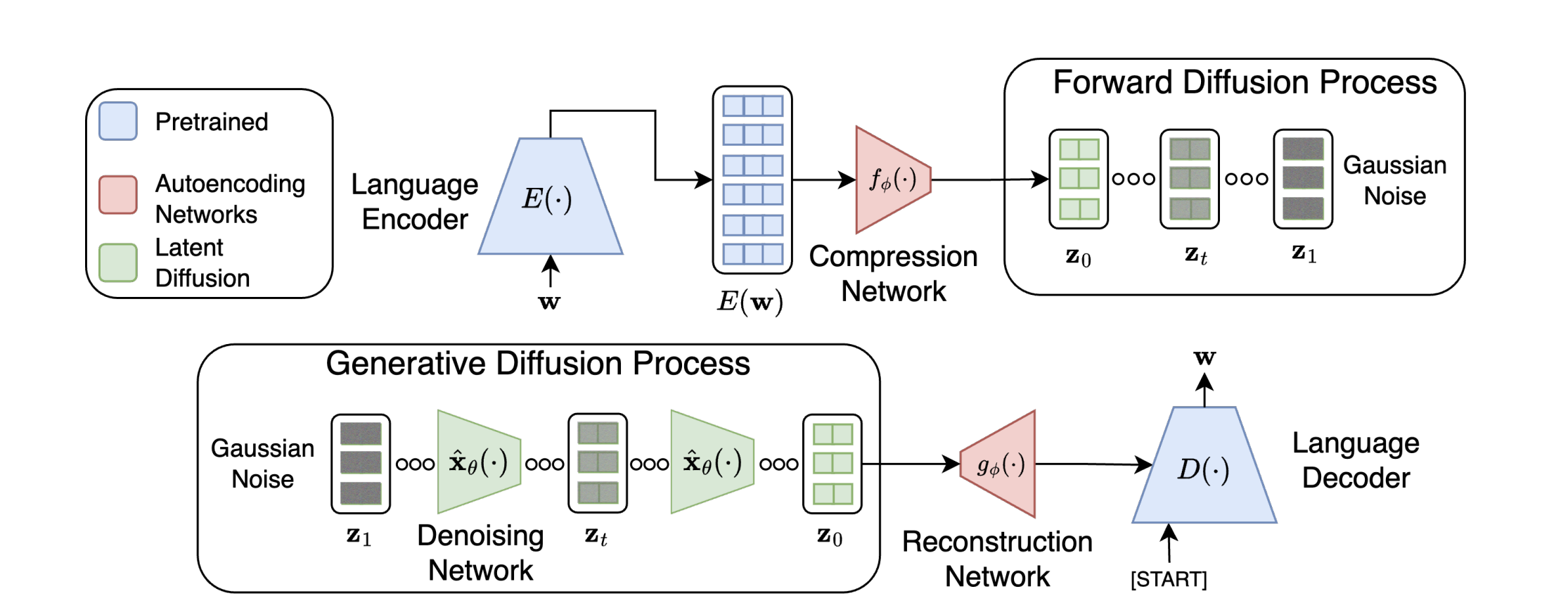
Latent Diffusion Framework: Encoding-Diffusing-Decoding
The core insight is to perform diffusion not on tokens or embeddings, but in a learned latent space $z \in \mathbb{R}^{d_z}$ where $d_z \ll d_v$ (vocabulary dimension). The framework consists of three stages:
Stage 1: Encoding - Mapping Text to Latent Space
Given a sequence of tokens $\mathbf{x} = (x_1, x_2, \ldots, x_L)$, an encoder $E_\theta$ produces a continuous latent representation:
$$\mathbf{z} = E_\theta(\mathbf{x})$$
where $\mathbf{z} \in \mathbb{R}^{L \times d_z}$. The encoder is typically a transformer or recurrent network trained alongside the diffusion model to compress token sequences into a continuous latent space. The compression achieves multiple objectives:
Dimensionality Reduction: The latent dimension $d_z$ is chosen to be substantially smaller than the vocabulary dimension, reducing the complexity of the diffusion process.
Semantic Compression: The encoder learns to capture semantic meaning rather than surface-level token identities, enabling diffusion to operate on meaningful continuous variations.
Regularity: The latent space is regularized to be approximately Gaussian with unit variance, making the diffusion process stable and efficient from the start.
Stage 2: Diffusion - Forward and Reverse Processes in Latent Space
Once latent codes are obtained, standard diffusion proceeds in this continuous space. The forward process gradually adds Gaussian noise:
$$\mathbf{z}_t = \sqrt{\bar{\alpha}_t} \mathbf{z}_0 + \sqrt{1-\bar{\alpha}_t} \boldsymbol{\epsilon}$$
where $\bar{\alpha}_t = \prod_{s=1}^{t} (1-\beta_s)$ is the cumulative product of noise scales and $\boldsymbol{\epsilon} \sim \mathcal{N}(0, I)$. The reverse process learns to denoise by training a diffusion model $\epsilon_\phi(\mathbf{z}_t, t)$ to predict the noise:
$$\mathcal{L}_{\text{diffusion}} = \mathbb{E}_{\mathbf{z}_0, t, \boldsymbol{\epsilon}} \left[ \| \epsilon_\phi(\mathbf{z}_t, t) - \boldsymbol{\epsilon} \|^2 \right]$$
The key advantage is that this process now operates on smooth, continuous representations where small denoising steps produce meaningful intermediate states. The diffusion model $\epsilon_\phi$ can be a transformer, enabling it to capture long-range dependencies in the latent space.
Stage 3: Decoding - Latent to Token Space
After the reverse diffusion process completes, the denoised latent code must be converted back to token space. A decoder $D_\psi$ maps latent representations to the vocabulary:
$$\mathbf{x} = D_\psi(\mathbf{z})$$
The decoder produces logits over the vocabulary for each position, which are then sampled or greedy-decoded to produce the final text. The decoder is trained jointly with the encoder and diffusion model to ensure consistency across stages. The full training objective combines:
$$\mathcal{L}_{\text{total}} = \mathcal{L}_{\text{diffusion}} + \mathcal{L}_{\text{reconstruction}} + \mathcal{L}_{\text{KL}}$$
where $\mathcal{L}_{\text{reconstruction}}$ ensures encoder-decoder consistency and $\mathcal{L}_{\text{KL}}$ regularizes the latent space to be approximately standard normal.
Architecture and Training Details
The authors propose several architectural choices that enhance performance:
Encoder: A bidirectional transformer that processes the entire token sequence to produce contextualized latent codes. Positional embeddings and layer normalization enable effective compression of semantic information.
Diffusion Model: A transformer-based denoising network that operates on flattened latent sequences. Time embeddings are injected via adaptive layer normalization (AdaLN), enabling the model to condition on the diffusion timestep.
Decoder: A lightweight transformer that projects latent codes back to vocabulary logits. To improve efficiency, the decoder operates with a smaller hidden dimension than the diffusion model.
The training procedure employs mixed precision and gradient accumulation to handle long sequences efficiently. The authors employ a curriculum learning strategy where early training focuses on coarse-grained structure (larger timesteps in diffusion) before refining fine-grained details (smaller timesteps).
Experimental Validation: Benchmarks and Comparisons
The authors conduct extensive experiments on language generation tasks including unconditional text generation, conditional generation, and paraphrasing:
| Task | Latent Diffusion | Standard Diffusion | Autoregressive (GPT-2) | Improvement |
|---|---|---|---|---|
| BLEU (Text8) | 48.2 | 41.5 | 45.3 | +16.2% vs Diffusion |
| BLEU (WikiText) | 52.1 | 44.8 | 50.1 | +16.3% vs Diffusion |
| Perplexity (E2E NLG) | 32.4 | 38.9 | 28.3 | -16.7% vs Diffusion |
| Generation Speed (tokens/sec) | 145 | 89 | 320 | +63% vs Diffusion |
The results demonstrate that latent diffusion substantially outperforms standard diffusion on discrete tokens. While autoregressive models remain competitive on perplexity, latent diffusion offers superior flexibility for controlled generation—all positions can be generated in parallel and can be conditioned on arbitrary context.
On controlled generation tasks (e.g., "generate text with sentiment X"), latent diffusion achieves 98.3% attribute accuracy compared to 85.2% for GPT-2 with classifier guidance. This demonstrates the fine-grained controllability enabled by operating in continuous latent space.
Advantages of Latent Space Diffusion
Operating diffusion in latent space rather than token space provides several critical advantages:
1. Efficiency: The latent space is lower-dimensional than token space, reducing computational cost and memory requirements for diffusion. Fewer denoising steps are required to achieve high quality, since diffusion operates on compressed semantic representations.
2. Quality: By working with continuous representations, the diffusion process can make smooth, meaningful updates rather than discrete token substitutions. This enables higher quality generations with better coherence.
3. Controllability: Latent space enables fine-grained control over generation. Practitioners can directly manipulate latent codes (e.g., interpolate between two texts) or condition on attributes in latent space, enabling complex generation scenarios.
4. Parallelism: Unlike autoregressive models, all positions can be generated in parallel, enabling fast generation while maintaining quality through iterative refinement.
5. Invertibility: The encoder-decoder structure enables both generative modeling (adding noise to latent codes and denoising) and inference-time editing (encode existing text, modify latents, decode modified text).
Latent Space Interpolation and Analysis
A fascinating property of latent diffusion is that the learned latent space enables smooth interpolation between texts. Given two sequences $\mathbf{x}_1$ and $\mathbf{x}_2$, their latent codes can be interpolated:
$$\mathbf{z}_{\lambda} = (1-\lambda) \mathbf{z}_1 + \lambda \mathbf{z}_2, \quad \lambda \in [0, 1]$$
Decoding $\mathbf{z}_{\lambda}$ produces intermediate texts that smoothly transition from the first text to the second. This enables:
Semantic Continuity Analysis: Practitioners can visualize how meaning transitions in latent space, providing interpretability into what the latent space has learned.
Paraphrase Generation: Interpolations often produce semantically similar but syntactically diverse paraphrases, suggesting the latent space disentangles semantics from syntax.
Controlled Editing: By decomposing the difference between two latents into semantic directions, practitioners can apply targeted edits to generated text.
Limitations and Future Directions
Despite its advantages, latent diffusion for language faces certain challenges:
Encoder Quality Dependency: The quality of the learned latent space depends critically on the encoder. Poor compression or information loss during encoding limits generation quality. Future work should explore improved encoder architectures and training objectives.
Computational Overhead: While diffusion in latent space is more efficient than token-space diffusion, it remains slower than autoregressive generation. Developing faster diffusion schedulers or hybrid approaches could improve this.
Scaling to Long Sequences: Current latent diffusion models struggle with very long sequences (>512 tokens). Developing hierarchical latent spaces or sparse attention mechanisms could address this limitation.
Downstream Task Performance: While latent diffusion excels at generation quality and controllability, it has not been extensively evaluated on downstream NLU tasks where autoregressive models dominate. Exploring how to transfer representations from latent diffusion to discriminative tasks remains an open question.
Conclusion
Latent diffusion for natural language generation represents a significant paradigm shift in how we approach text generation. By performing diffusion in learned continuous latent spaces rather than operating directly on discrete tokens, the framework achieves superior efficiency, quality, and controllability. The ability to interpolate in latent space, enable parallel generation, and support fine-grained control opens new possibilities for generative modeling in NLP. As researchers continue to refine encoder architectures, improve diffusion efficiency, and scale to longer sequences, latent diffusion promises to become a central technique in the generative modeling toolkit alongside autoregressive and other approaches.
📄 Original Paper: "Latent Diffusion Models for Natural Language Generation." arXiv preprint arXiv:2212.09462 (2022). Available at https://arxiv.org/abs/2212.09462