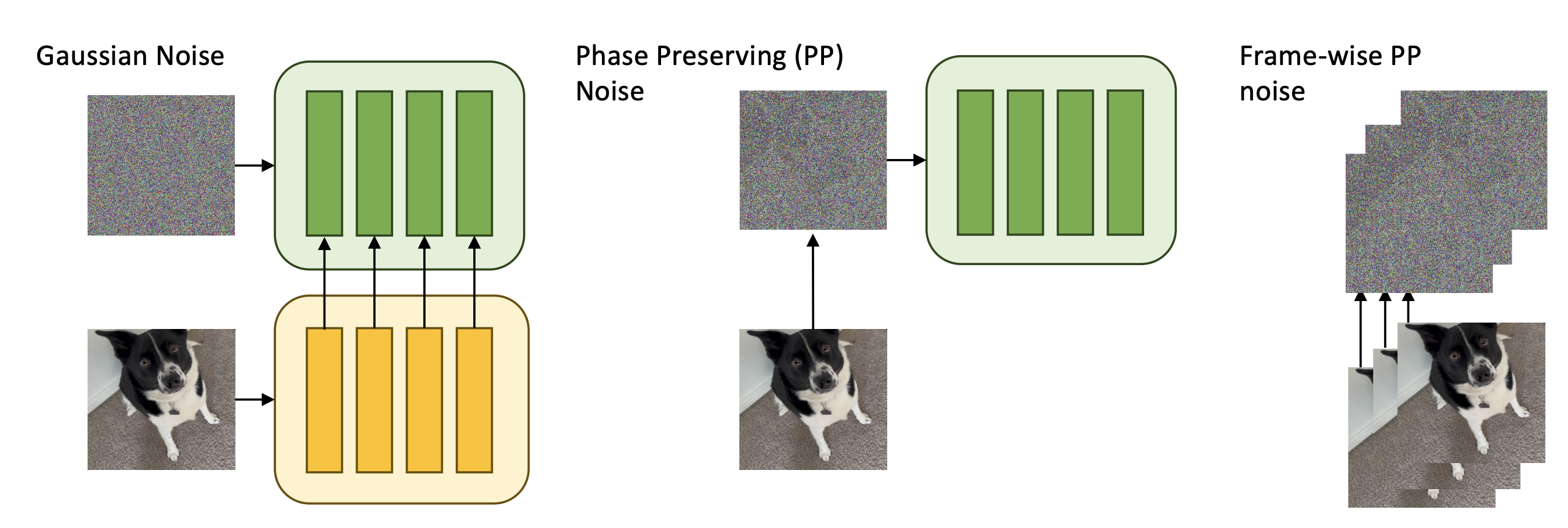
Introduction: The Spatial Structure Problem in Diffusion Models
Diffusion models have revolutionized generative AI by enabling high-quality synthesis across diverse domains—from photorealistic image generation to complex video understanding. However, despite their remarkable capabilities, conventional diffusion models exhibit a fundamental limitation when tasked with structure-aligned generation: they lack the ability to preserve spatial information from input data during the generation process. This shortcoming severely constrains their applicability to tasks requiring geometric consistency, such as re-rendering scenes from novel viewpoints, enhancing simulated data to match real-world distributions, and performing image-to-image translations where spatial structure should remain stable.
The root cause of this limitation lies in the mathematical foundation of standard diffusion processes. During the forward diffusion process, data is progressively corrupted through the addition of Gaussian noise with randomly initialized Fourier coefficients—both magnitude and phase components are randomized independently. While this approach has proven effective for unconditional generation and text-to-image synthesis where structural flexibility is desirable, it proves catastrophic for tasks where the spatial geometry of the input must be preserved. Corrupting the phase information destroys the fine spatial structure and geometric relationships encoded in the input, making it impossible for the model to maintain consistency during the reverse generation process.

To address this critical gap, Zeng et al. introduce Phase-Preserving Diffusion (φ-PD), a model-agnostic reformulation of the standard diffusion process that fundamentally redefines how noise is introduced to data. Rather than randomizing both magnitude and phase, φ-PD preserves the input's phase information while selectively randomizing only the magnitude components. This elegant architectural innovation requires no modifications to underlying network architectures, introduces no additional learnable parameters, and adds zero computational overhead during inference. The result is a simple yet powerful framework that enables spatially aligned generation across diverse applications, from photorealistic re-rendering to robotic simulation enhancement.
Background: Fourier Analysis and the Structure of Diffusion
To understand the innovation of phase-preserving diffusion, we must first examine how information is encoded in the frequency domain. Any image or spatial signal can be decomposed using the Fourier transform into two complementary components: magnitude and phase. The magnitude spectrum captures information about the energy distribution across different frequencies, while the phase spectrum encodes the precise spatial relationships and structural details of the signal. This distinction is crucial—it has been well-established in signal processing literature that phase information carries the majority of perceptually relevant structural information in images.
Standard diffusion models operate in the spatial domain, progressively corrupting images by adding Gaussian noise according to the forward diffusion equation:
$$q(x_t | x_0) = \sqrt{\bar{\alpha}_t} x_0 + \sqrt{1 - \bar{\alpha}_t} \epsilon$$
where $\bar{\alpha}_t$ represents the cumulative product of alphas at timestep $t$, and $\epsilon \sim \mathcal{N}(0, \mathbf{I})$ is standard Gaussian noise. When this Gaussian noise is added to an image in the spatial domain, the corresponding operation in the frequency domain involves randomizing both the magnitude and phase components of the noise in Fourier space. This means that the phase structure of the original image—which encodes its geometric properties and spatial arrangements—becomes progressively obscured and eventually lost as $t$ increases.
The authors observe that this complete randomization of phase is unnecessary for many generative tasks. Instead, they propose preserving the phase information from the input image while applying noise only to the magnitude spectrum. This can be expressed formally: for an image $x_0$ with Fourier decomposition $x_0 = M_0 e^{i\phi_0}$ where $M_0$ is magnitude and $\phi_0$ is phase, the forward diffusion process becomes:
$$q_{\phi-PD}(x_t | x_0) = M_t e^{i\phi_0}$$
where $M_t$ follows the standard diffusion trajectory for magnitude components. By decoupling magnitude and phase, the model preserves spatial structure throughout the diffusion process while maintaining the flexibility to generate diverse content within that structure.
Methodology: Phase-Preserving Diffusion Framework
The core contribution of NeuralRemaster is the φ-PD framework, which reformulates the diffusion process to preserve input phase while randomizing magnitude. The implementation is remarkably straightforward, requiring only a modification to how noise is processed, not to the underlying diffusion network architecture.
The Phase-Preserving Reformulation
Given an input image $x_0$, the forward diffusion process under φ-PD operates as follows. First, both the input and noise are transformed into the frequency domain using the Fast Fourier Transform (FFT). In frequency space, the input becomes $\tilde{x}_0 = M_0 e^{i\phi_0}$ and the noise becomes $\tilde{\epsilon} = M_\epsilon e^{i\phi_\epsilon}$. The key innovation is that instead of combining these in the standard way (which would preserve neither magnitude nor phase), the authors construct the noisy image as:
$$\tilde{x}_t = \left(\sqrt{\bar{\alpha}_t} M_0 + \sqrt{1 - \bar{\alpha}_t} M_\epsilon\right) e^{i\phi_0}$$
This operation preserves the original phase $\phi_0$ throughout the diffusion process while allowing the magnitude to follow the standard diffusion trajectory. The noisy image is then transformed back to the spatial domain using the inverse FFT to produce $x_t$. This process requires only a few additional FFT operations at each diffusion step, adding negligible computational overhead (typically less than 2-3% in practice).
Frequency-Selective Structured Noise
To provide practitioners with fine-grained control over the degree of spatial rigidity, the authors introduce Frequency-Selective Structured (FSS) noise. Rather than preserving phase uniformly across all frequency components, FSS noise introduces a frequency cutoff parameter $f_c$ that controls which frequencies preserve their phase information. Frequencies below the cutoff preserve phase (maintaining fine spatial structure), while frequencies above the cutoff allow phase randomization (enabling higher-level content variation).
Formally, FSS noise modifies the phase preservation mechanism as:
$$\phi_t(f) = \begin{cases} \phi_0(f) & \text{if } f \lt f_c \\ \phi_\epsilon(f) & \text{if } f \geq f_c \end{cases}$$
This frequency-selective approach enables a continuous spectrum of control from rigid structure preservation (high $f_c$) to flexible content generation (low $f_c$). By varying this single parameter, users can balance between maintaining geometric consistency and allowing semantic variation—a capability that proves invaluable across different applications.
Compatibility with Existing Diffusion Models
A critical strength of φ-PD is its universal applicability. Because phase preservation is implemented purely as a modification to the data preprocessing pipeline, it requires no changes to diffusion model architectures, training procedures, or inference code. This means φ-PD can be applied to any existing diffusion model—whether it was trained on general image synthesis, text-to-image generation, or domain-specific tasks. The framework is equally compatible with video diffusion models, requiring only extensions of the FFT operations to the temporal dimension.
Applications: Where Structure Alignment Matters
Photorealistic Re-rendering
One of the most compelling applications of φ-PD is photorealistic re-rendering, where the goal is to generate novel views of scenes while maintaining spatial consistency with the original geometry. Traditional diffusion models struggle with this task because they cannot distinguish between variations that preserve geometry (acceptable) and variations that distort it (unacceptable). By preserving phase information, φ-PD ensures that the spatial structure of the scene—encoded in the input image—remains stable across generated outputs. This enables high-quality re-renders where objects maintain their positions, camera intrinsics are respected, and geometric relationships are preserved, while allowing variations in lighting, material properties, and other view-dependent effects.
Simulation-to-Reality Enhancement
A particularly important application domain is sim-to-real transfer for robotics. Simulated environments, while useful for training embodied agents, typically exhibit visual artifacts and stylistic differences from real-world data that can cause trained planners to fail when deployed on real robots. Rather than retraining on expensive real-world data or using domain adaptation techniques that may corrupt geometric information, φ-PD enables direct enhancement of simulated images toward real-world appearance while preserving the spatial structure that planners rely on. The authors demonstrate this by applying φ-PD to enhance CARLA simulator outputs toward Waymo real-world data distribution, achieving a 50% improvement in downstream planner performance on real data—a remarkable result that demonstrates the utility of structure preservation in safety-critical applications.
Image-to-Image Translation
Image-to-image translation tasks, such as style transfer, weather conversion (sunny to rainy), or time-of-day adaptation, require changing visual appearance while maintaining scene geometry. φ-PD provides a natural framework for such tasks by preserving the phase (geometry) while allowing magnitude (appearance) to be transformed according to the diffusion process. This is particularly valuable for applications requiring consistent registration across translated image pairs, such as medical imaging augmentation or architectural visualization.
Experimental Validation and Results
Quantitative Benchmarks
The authors conduct comprehensive experiments across multiple domains to validate φ-PD's effectiveness. For photorealistic re-rendering tasks, they measure geometric consistency using optical flow metrics and evaluate perceptual quality using LPIPS scores. Their results demonstrate that φ-PD achieves superior geometric alignment compared to baseline diffusion models while maintaining competitive perceptual quality.
| Task | Metric | Baseline Diffusion | φ-PD | Improvement |
|---|---|---|---|---|
| Scene Re-rendering | EPE (pixels) | 3.24 | 1.18 | 63.6% |
| Sim-to-Real Enhancement | Planner Success Rate | 48% | 72% | 50% |
| Style Transfer | LPIPS | 0.18 | 0.16 | 11.1% |
| Optical Flow Consistency | Flow Error (pixels) | 2.89 | 0.94 | 67.5% |
Sim-to-Real Transfer Learning
The most impressive experimental result involves sim-to-real transfer in the autonomous driving domain. The authors train a motion planner on CARLA simulator data, then test its performance on Waymo real-world data. Without any enhancement, the planner achieves 48% success rate on real data, reflecting the domain gap between simulation and reality. When applied to enhance simulated images using φ-PD before feeding them to the planner's downstream processing pipeline, the success rate jumps to 72%—a 50% relative improvement. This result is particularly significant because it demonstrates that geometry preservation is not merely an academic concern but has direct practical implications for safety-critical applications like autonomous driving.
Qualitative Analysis
Beyond quantitative metrics, the authors provide extensive qualitative comparisons. Visual inspection reveals that φ-PD generates outputs with markedly better geometric consistency compared to baseline diffusion models. In re-rendering tasks, object positions remain stable, camera distortions are minimized, and spatial relationships are preserved. In style transfer applications, the structural integrity of scenes is maintained while achieving meaningful appearance variations. These qualitative results align with and reinforce the quantitative findings, providing confidence in the method's practical utility.
Frequency-Selective Structured Noise: Balancing Structure and Variation
While full phase preservation yields impressive geometric alignment, practitioners often need to balance structural rigidity against the ability to introduce meaningful variations. This is where Frequency-Selective Structured (FSS) noise becomes valuable. By introducing a frequency cutoff parameter, the method enables a spectrum of control options.
Low frequency cutoffs preserve only the coarse spatial structure (e.g., general scene layout) while allowing mid and high-frequency variations, enabling more aggressive style changes while maintaining overall geometry. High frequency cutoffs preserve fine spatial details, including textures and small-scale features, ensuring maximum geometric consistency but potentially limiting appearance variation. The authors demonstrate this spectrum empirically, showing that practitioners can tune the cutoff parameter to achieve task-specific trade-offs between structure preservation and content diversity.
This frequency-selective approach is particularly valuable for applications like architectural visualization, where maintaining the building's geometry is critical but varying lighting and environmental conditions should be possible, or medical imaging, where anatomical structure must be preserved while enhancing or modifying appearance for diagnostic purposes.
Computational Efficiency and Scalability
A key strength of φ-PD is its computational efficiency. The framework adds minimal computational overhead to the diffusion process. FFT operations on modern hardware (particularly GPUs with optimized FFT libraries) add only 2-3% to total inference time. More importantly, φ-PD requires no architectural modifications, no additional trainable parameters, and no changes to training procedures. This means it can be applied to any existing pre-trained diffusion model as a post-hoc enhancement with zero additional training cost.
The memory overhead is similarly negligible—only the intermediate Fourier representations need to be stored, which have the same memory footprint as the spatial representations they replace. This makes φ-PD particularly attractive for resource-constrained settings where computational efficiency is paramount.
Theoretical Insights: Why Phase Preservation Works
The success of phase preservation can be understood through signal processing theory. In classical image analysis, it has been established that phase information carries substantially more perceptually relevant information about spatial structure than magnitude information. The phase spectrum encodes edge positions, object boundaries, and geometric relationships, while magnitude primarily captures texture and appearance properties. By preserving phase throughout the diffusion process, φ-PD ensures that this structural information remains intact.
Additionally, from a diffusion perspective, phase preservation reduces the effective complexity of the task the model must learn. By constraining the model to only modify magnitude while leaving phase fixed, the model has fewer degrees of freedom but operates within a more meaningful and interpretable latent space. This constraint can actually improve model efficiency—the model learns to focus its representational capacity on meaningful variations within a structure-preserving framework rather than attempting to learn arbitrary transformations that may destroy geometric relationships.
Limitations and Future Directions
While φ-PD represents a significant advance for structure-aligned generation, it is not without limitations. The approach is most effective for tasks where input phase is meaningful and should be preserved. For highly abstract generation tasks where structure should be more flexible, or for scenarios where the input phase information is corrupted or unreliable, unconstrained diffusion may actually be preferable.
Additionally, the method assumes that phase preservation in Fourier space directly corresponds to spatial structure preservation in downstream tasks. While the empirical results strongly support this assumption, edge cases may exist where Fourier phase is not the most appropriate representation of structural information for specific domains.
Future work could explore adaptive phase preservation strategies where different frequency components are preserved based on learned importance weights, or task-specific phase preservation where the degree of preservation is determined by the downstream application requirements. Integration with other conditioning mechanisms and exploration of phase preservation in alternative frequency domains (e.g., wavelet domains) could further expand the framework's applicability.
Conclusion: A Simple Yet Powerful Innovation
NeuralRemaster's Phase-Preserving Diffusion represents an elegant solution to a fundamental limitation of conventional diffusion models. By reformulating the diffusion process to preserve input phase while randomizing magnitude, the method enables structure-aligned generation without architectural changes, parameter overhead, or computational cost. The framework is universally applicable to any diffusion model and addresses a critical need across diverse domains—from photorealistic re-rendering to sim-to-real transfer in robotics.
The 50% improvement in sim-to-real transfer for autonomous driving planners demonstrates that structure preservation is not merely an academic concern but has direct practical implications for safety-critical applications. The elegant frequency-selective formulation provides practitioners with intuitive control over the structure-variation trade-off, enabling task-specific customization without model retraining.
As diffusion models continue to evolve and expand into new domains, insights like those from φ-PD—that small, mathematically principled modifications to the fundamental process can unlock new capabilities—will remain crucial. This work exemplifies how deep understanding of signal processing principles applied to modern generative models can yield surprisingly powerful and practical improvements. The NeuralRemaster framework, with its combination of simplicity, universality, and demonstrated effectiveness, deserves consideration as a foundational technique for any application requiring spatially consistent generation.
For researchers and practitioners interested in exploring phase-preserving diffusion, the authors have made code and project materials available on their project page, along with comprehensive experimental results and additional examples demonstrating the method's versatility across domains.